The extremely large telescope (ELT) is a telescope currently under design/construction. With its 39 meter wide segmented primary mirror, once finished, it will be the largest optical telescope built. Once it will start to collect photons it will open new frontiers and extend mankinds knowledge about the universe. It’s a project with collaboration across the globe involving many universities, industries and organizations. It’s a mighty instrument including many fields of engineering such as electrical-, mechanical-, optical- and software engineering. Alright you get it. The ELT is big, cool and everything… but what does that have to do with the TwinCAT automation interface?
When working in a large project you usually come to a point where some processes need to be automated in order to save time and increase quality of the deliverable. Anyone that has worked with the development of TwinCAT software knows that there are several steps involved to even create the most basic project and deploy it on to a target device. These steps include, but are not limited to:
- Defining the realtime properties
- Writing unit tests
- Creation of POUs/business logic/writing software
- Defining the I/O and linking them to the instances of the POUs
- Installing and referencing libraries (both TwinCAT system and own)
- Configuring the target and installing any necessary software (IP-addresses, OPC-UA server, etc)
- Creating an AMS-route to the target
- Selecting the target for deployment of the software
- Activating configuration on the target
Everything that is not in bold is a one-time activity. The project is created, worked on for some time and properly tested on unit-, integration- and system level. Using version control, tags are created for all involved artifacts and we have a deliverable that is well-tested and with a minimum amount of bugs. But what about the activities in bold? This is something that needs to be created for each and every individual target (PLC). These activities aren’t particularly time consuming if you only need to do it for one, two or maybe three PLCs. But what if you need to do it for 132 PLCs? Well, then you have two choices:
- Manually do it using the processes and tools that you are used to, which involves manually using the TwinCAT XAE for each and every target
- Automate it
One specific subsystem in the ELT has 132 identical PLCs, and doing this manually would mean that any upgrade of the software would require tons of work. Because it involves human intervention in every step of the process, it’s prone to errors. Also, doing any upgrade (even minor ones) would require up to a week of work. When the ELT is finished, astronomers all over the world will want to get observation time of it, as demand will be overwhelmingly larger than the supply of observation hours. If we would need to do an upgrade of the software in the PLCs that would require the ELT to be shutdown for days, it would most likely mean a couple of things:
- a lot of work would have to be done manually that would take a long time meaning that…
- the astronomers would get quite sad meaning that…
- less science would be done
We don’t want that to happen, because we want the ELT to be a highly productive instrument collecting tons of science. Any upgrade needs to be done during the day between observation runs, meaning that not a single second of observation time can be lost because of software upgrades of the PLCs. The only way to realize this is to automate this process.
This post is part one of three about this specific problem and how it was solved using the automation interface. While this part is more focused on describing the use case, we will look at the more practical aspect of the problem and look at a solution using the automation interface. I will limit the scope of this series to the creation of AMS-routes and deploying the target on the PLCs. Initial configuration and installation of the PLCs can be automated too, but will simply have to wait for another series of posts.
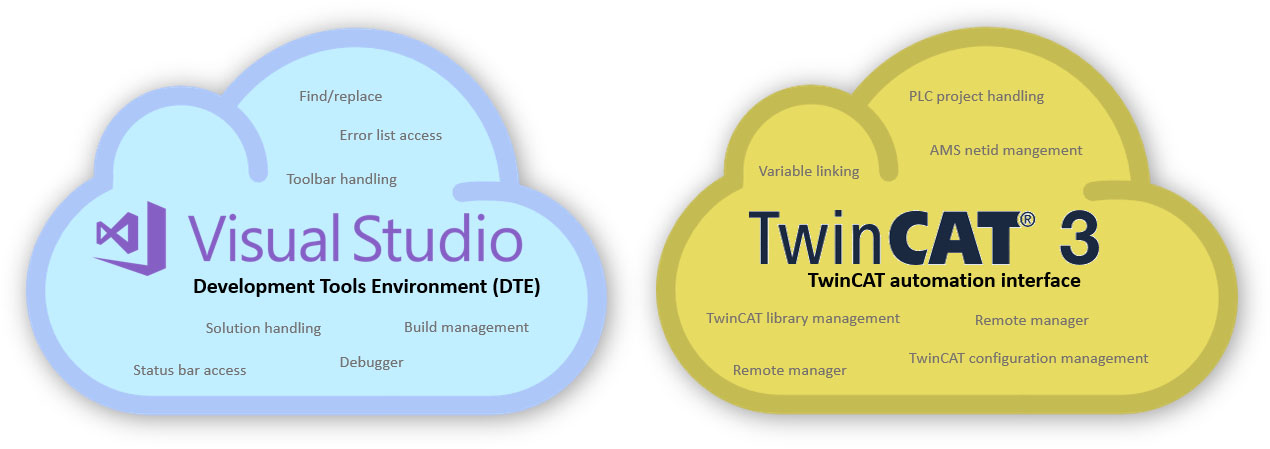
So how do we go on to automate the processes involved in the deployment of the software to the PLCs? With the TwinCAT3 integrated development environment being integrated in Visual Studio this will be our playground. In order for us to access the functionality of Visual Studio programmatically Microsoft has created something called the Development Tools Environment (DTE). Much of the things that we take for granted in TwinCAT such as build/rebuild/clean are natural parts of Visual Studio and can be accessed through the DTE. The DTE does however not give access to the things that are specific for TwinCAT, which is quite a great amount of functionality. Everything related to creation of task creation, PLC projects, I/O configuration, TwinCAT library referencing, compilation, target selection, activation of configuration to target and much more. To access TwinCAT specific functionality, we need to use the TwinCAT automation interface. I want you to think of the TwinCAT automation interface as a door that gives you access to most TwinCAT specific functionality in visual studio, but without requiring any human to do all the clicks in visual studio but rather doing it programatically from a machine.
We also need to have a testing environment to test our software at. For this we’ve got three different options:
- Option one would be to wire up all 132 PLCs
- The second option is to just try this with two or more PLCs, as anything more than one is enough to test proof-of-concept
- The last option is to do it by virtualization
Option one is obviously not feasible, as this is highly impractical and, in most cases, not even possible because of resource limitations. Option two is good, and is an alternative that you usually want to try out in the end. The best alternative for this case is however option 3. Because Beckhoff PLCs are basically standard PCs, the runtime can be running in a virtual machine running Windows7/10. I think the virtualization possibility with TwinCAT3 is such a huge selling point that I’ve written a separate post about it that I urge you to read. Because the VMs doesn’t cost us anything, we can create as many as we want (given we have the horsepower of a machine to support it). Running TwinCAT3 in a virtual machine has the obvious drawback of that the realtime properties are terrible, but for this purpose and test of doing mass-deployment of software it does not matter at all! I’m not going to run the programs for the purpose of doing performance tests. I just want the virtual machine to behave like a PLC from the deployment point of view. We just basically need to create one single virtual machine with TwinCAT3 installed, and make as many clones of it as we want (though with different IP-addresses and AMS-NetIds). The possibility for me to run TwinCAT3/ADS in a virtual machine as if it was a normal PLC is such a great feature for me when developing software for the ELT that I can’t stress it enough! Honestly, I don’t think Beckhoff really understands how big of a selling point this is for them.
In the next part we will be more practical and look at the bits and pieces of how to use the automation interface to solve our problem by creating a .NET C# project.
A concept view of the ELT by ESO from www.eso.org